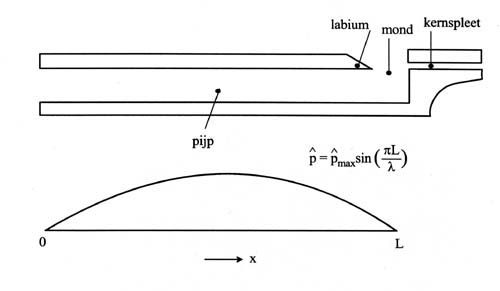
|
Figuur 1: Geometrie van een blokfluit en akoestische druk-amplitudeverdeling van de grondtoon |
Het fysisch modelleren van muziekinstrumenten staat sterk in de belangstelling. Instrumentenbouwers gebruiken de modellen om de klank van hun instrumenten te verbeteren; anderen proberen de klank van muziekinstrumenten zo goed mogelijk elektronisch na te bootsen. Blaasinstrumenten zijn lastig te modelleren omdat de karakteristieke klank wordt bepaald door de niet-lineaire dynamica van wervelende luchtstromingen in het instrument. Laboratoriumexperimenten laten zien hoe deze luchtwervels zich gedragen in een blokfluit of orgelpijp.
In een muziekinstrument ontstaat een toon doordat een bron (hamer, strijkstok, hand) een resonator (snaar, stemvork) in trilling brengt. Maar zonder een zogenaamde `straler' kunnen we die toon nauwelijks horen: om trillingen van een stemvork waar te nemen houden we de vork tegen een tafel of tegen de klankkast van een muziekinstrument. Per trillingsperiode wordt een fractie van de trillingsenergie van de resonator overgedragen op de straler, die het efficiënt in akoestische golven omzet. De straler is een `impedantie'-aanpassing tussen het instrument en de omgevingslucht (zie kader).
Bij een piano wordt een snaar impulsief in trilling gebracht met behulp van een hamer. Er ontstaan `vrije' trillingen van de snaar die overeenkomen met de eigenfrequenties van deze resonator. De snaren dragen trillingsenergie over aan de harmonietafel die als straler fungeert. Hoewel er zeer subtiele koppelingseffecten optreden tussen de bron, de resonator en de straler, kunnen deze drie systemen als vrijwel onafhankelijk beschouwd worden [1].
Bij een strijkinstrument drijft een continue beweging van de strijkstok een oscillerende beweging van de snaar aan. Dit is het gevolg van een sterke niet-lineaire wrijvingskarakteristiek van de strijkstok op de snaar: de snaar wordt afwisselend meegetrokken en losgelaten door de strijkstok . De trilling wordt dus in stand gehouden door een sterke interactie tussen bron en resonator. Deze niet-lineaire interactie zorgt er ook voor dat de snaartrilling periodiek is, maar niet zuiver sinusoidaal. In tegenstelling tot piano's en andere slaginstrumenten zijn de boventonen van een strijkinstrument daardoor automatisch zuivere `harmonischen' van de grondtoon: hun frequentie is een veelvoud van de grondtoonfrequentie. Het geluid klinkt dan ook helderder dan bij de meeste slaginstrumenten. Hoewel de interactie tussen bron en resonator van een strijkinstrument sterk is, blijkt de koppeling tussen de snaar en de klankkast juist heel zwak te zijn. Als dat niet het geval is ontstaan er gekke bijgeluiden en is het instrument onbespeelbaar. Deze `wolftonen' treden op wanneer een eigenfrequentie van de klankkast te dicht bij een snaarfrequentie ligt.
De fluit
Fluiten en orgelpijpen zijn muziekinstrumenten waarbij een dunne luchtstraal tegen een scherpe rand, het labium, wordt geblazen [2]. We noemen ze labiaalinstrumenten. De geometrie van een labiaalinstrument is schematisch weergegeven in figuur 1.
|
|
|
|
Bij een blokfluit wordt de luchtstraal gevormd aan de uitgang van een dun kanaal, de kernspleet. De uitgang van de kernspleet zit aan de rand van de `mond', een opening in de zijwand van de pijp. Het labium is de tegenoverliggende rand van de mond.
Bij het blazen met voldoende hoge en constante druk wordt een stabiele akoestische trilling in de pijp opgewekt. De oscillerende druk in de pijp gaat gepaard met dichtheidsveranderingen. Dit betekent dat afwisselend lucht de pijp instroomt of uitgespuugd wordt, zowel bij de mond als bij het andere open pijpeinde. Hierdoor ontstaat dwars op de luchtstraal in de mond een oscillerende stroming, die de luchtstraal tussen de mond en het labium verstoort.
In figuur 2 is deze stroming zichtbaar gemaakt in een experimentele opstelling.
|
|
|
Rond het labium ontstaan wervelstructuren die vergelijkbaar zijn met de oscillaties van een rookpluim boven een sigaret die men in een trillende hand houdt. De beweging van de luchtstraal om het labium en de wervelafschudding aan het labium zorgen voor de productie van akoestische energie die de pijposcillaties in stand houdt. De bron en de resonator zijn dus sterk met elkaar verweven. De interactie tussen de pijp en de luchtstraal is te beschrijven als een terugkoppellus met de straal als versterker en de pijp als filter. De mechanische trilling van het labium is hierbij verwaarloosbaar.
In het verleden is de geluidsproductie in een fluit vaak beschreven als een `randtoon' gekoppeld aan een akoestische resonator. Een randtoon is de fluittoon die onstaat wanneer je in afwezigheid van een resonator tegen een scherpe rand blaast. Zo'n model is een poging om de geluidsbron als een zelfstandig systeem te beschouwen, maar het heeft weinig voorspellende waarde: een moeilijk verschijnsel wordt verklaard in termen van iets dat men ook niet echt begrijpt [3]. Bovendien blijkt uit stromingsvisualisaties, zoals die van figuur 2, dat de stroming in de mond van een blokfluit sterk afwijkt van die in een randtoon-configuratie .
Wervelstructuren
Net als bij een viool zijn de bron en de resonator in een fluit dus sterk gekoppeld.
Toch kunnen we deze functies apart beschrijven omdat ze op verschillende lengteschalen
werken. Het gebied waarin geluid wordt opgewekt in de mond heeft een lengteschaal van
millimeters, terwijl de pijp tientallen centimeters lang is. Akoestische
golfverschijnselen die in de pijp domineren, zijn verwaarloosbaar bij de mond. Er is een
nog sterker verschil tussen de stroming in de pijp en in de mond, dat met de aard van de
bron te maken heeft. Zoals gesteld door Rayleigh [5] kan een staande golf bij een drukknoop (in de mond) niet
aangedreven worden door een volume-injectie van inkomende lucht, omdat er in zo'n knoop
geen druk aanwezig is: de volume-injectie verricht geen arbeid (
omdat 
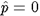) . De
geluidsbron moet daarom een kracht zijn. Men kan deze kracht formeel identificeren als de
Coriolis-kracht die een waarnemer ondervindt in wervelstructuren zoals we zien in figuren 2 en 3 ([4], [7]). In deze moderne benadering, de aëro-akoestiek, wordt
het akoestisch veld gedefineerd als de tijdafhankelijke, niet-roterende component van het
stromingsveld. Afwijkingen hiervan, de wervels, zijn geluidsbronnen. Dit levert formeel
een scheiding tussen de geluidsbron en de akoestische staande golf in de resonator.
Hoewel de stroming in de pijp voornamelijk bepaald wordt door de grondtoon, is deze voor ons oor nauwelijks hoorbaar. De uitstraling van akoestische golven door de mond en het andere open einde van de pijp zijn bij de grondtoon namelijk zeer inefficiënt, omdat deze openingen veel kleiner zijn dan de golflengte van de toon. Er verdwijnt meer akoestische energie in wandwrijving dan er uitgestraald wordt [4]. De uitstraling wordt dus voornamelijk bepaald door de boventonen, terwijl in de resonator de grondtoon domineert. Ook blijkt ons oor niet erg gevoelig te zijn voor zulke lage frequenties. We zijn vooral gevoelig voor het frequentiegebied rond 3 kHz [1]. Hoewel de drukamplitude van de grondtoon in de pijp honderd keer zo groot is als die van de vijfde harmonische, zijn beide van vergelijkbaar belang voor ons oor. We horen de hogere harmonische veel beter (factor 3) en deze wordt door de fluit ook veel beter uitgestraald (factor 25).
Dynamisch gedrag
De tonen van een blokfluit worden dus gevormd door de kleine hoogfrequente afwijkingen van de harmonische oscillatie in de fluit. Zulke hoge frequenties worden veroorzaakt door kleine abrupte gebeurtenissen die veel sneller variëren dan de globale stroming die de grondtoon aandrijft. De frequentieverdeling van hogere harmonischen en de aanwezigheid van ruis zorgen ook voor de klankkleur van het instrument. Daarnaast speelt het dynamisch gedrag van het instrument een grote rol bij onze perceptie van muzikaal geluid [1].
Een voorbeeld van het belang van dynamisch gedrag en ruis is het verschil tussen de perceptie van klarinetgeluid en het geluid van een orgelpijp. In beide gevallen worden de boventonen gedomineerd door de oneven harmonischen van de grondtoon. De klarinet heeft echter een zeer korte aanzet: binnen enkele trillingsperioden is een stabiel periodiek geluid bereikt. Maar een orgelpijp start vaak op een boventoon, om daarna langzaam over te gaan naar de grondtoon. Deze overgang kan dertig oscillatie-perioden duren. Ook is de turbulente ruis een belangrijke component van het geluid, vooral bij orgelpijpen en dwarsfluiten. Gelukkig is het mogelijk om realistische ruis aan een numerieke simulatie toe te voegen zonder een exact model te hanteren [7].
Hoewel de bron, de resonator en de straler in een fluit dus sterk met elkaar verweven zijn, kunnen ze toch met onafhankelijke fysische modellen beschreven worden, omdat er grote verschillen zijn in de lengte- en tijdschalen die bij elk van deze functies horen. We kunnen bijvoorbeeld een eenvoudig laagfrequent model gebruiken om het dynamische gedrag van het instrument te voorspellen. Met behulp van zo'n `karikatuur' was Verge in staat om een realistische `virtuele' fluit te bouwen. Een origineel aspect van dit werk is dat voor het eerst [7] de geluidsproductie tijdens de aanzet werd geanalyseerd (figuur 3).
|
|
|
Net als bij een echt instrument moeten echter kleine aanpassingen van het model gebruikt worden om het instrument op het gehoor te intoneren. Ons oor blijft het meest gevoelige en kritische meetinstrument!